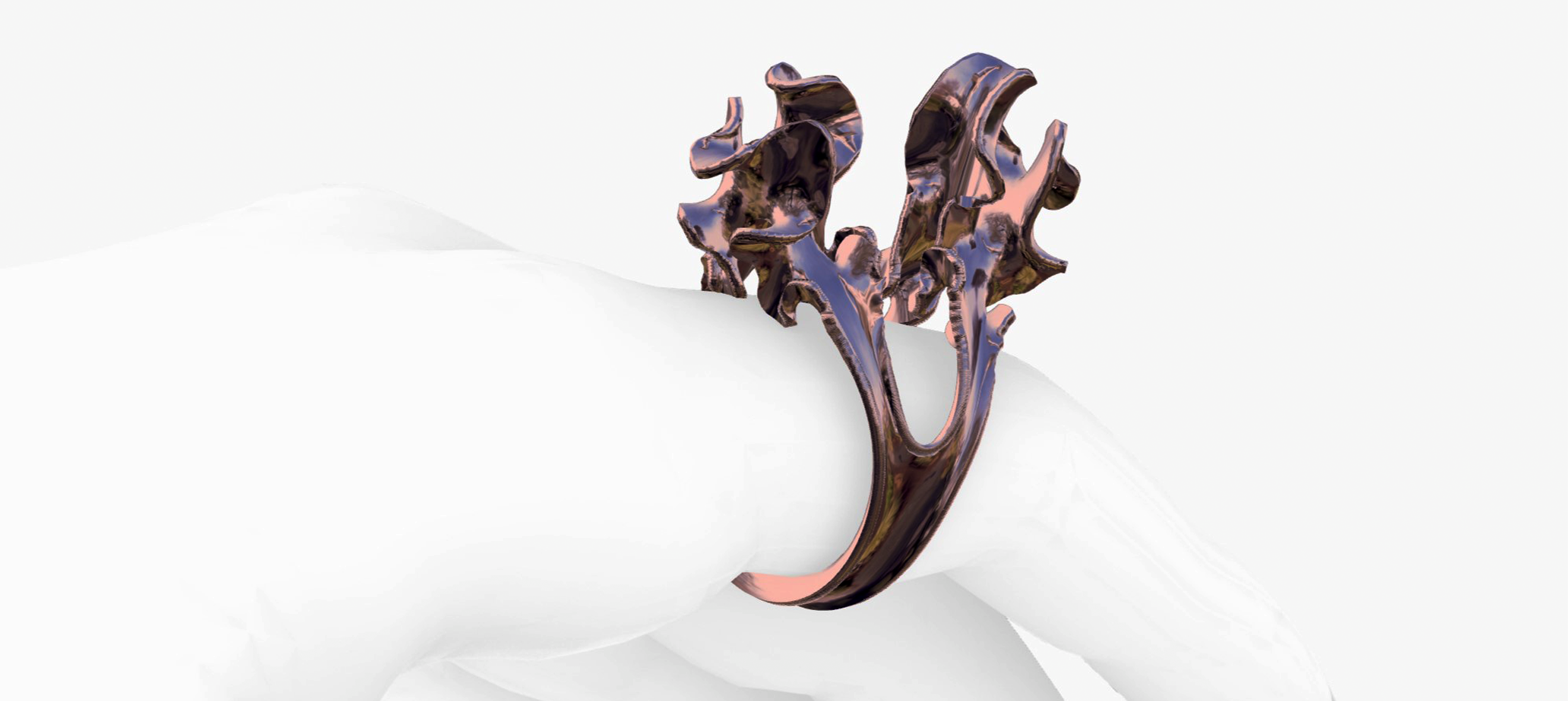
Differential Growth
This study was initiated by Andrei Padure from Digital Matters. It inspired me to dig more inside the growth process of hyperbolic geometry seen in nature, on land, and in oceans. How does an organism go from a simple geometry of one cell to a highly differentiated geometry of billions of cells? How does it grow? Some may say "by division and subdivision,"... But how? Growth is not a uniform process, and as we see it, some parts grow more than other parts. It is a highly differentiated subdivision process with particular rules for each growth stage. Natural growth cannot exclude external factors like heat, light, gravity, and humidity. Scientists say rippled leaves are like surfaces growing differentially from their edge. That means the growth algorithm goes around this specific rule.
The growth simulation used Grasshopper basic, Anemone for the iterative process, and Weaverbird for refining the final shape (mesh). The script has two distinct parts:
1. The first step in the growth process is to double the number of vertices for each loop and move them outside the initial geometry (simulating the cell division from the natural environment).
2. The second part performs the collision check (avoid neighbor leaves!), calculating the forces from each vertex to its neighbors. All forces are added, and the mean force moves the vertices outside. The attractor or any other exterior factor (solar and radiation analysis, gravity, wind, humidity ) can also add values to the initial set of forces feeding and differentiating the growth process.
There are two different types of growth. For each case, one attractor was used to choose which part grows more than the other.
A. The growth with a small length segment and highly iterated.
B. The growth with a bigger length segment and a small number of iterations.
.webp)

